자바칩
[백준 / Java] 14500: 테트로미노 (구현, 백트래킹) 본문
난이도: Gold 4
문제: https://www.acmicpc.net/problem/14500
문제
폴리오미노란 크기가 1×1인 정사각형을 여러 개 이어서 붙인 도형이며, 다음과 같은 조건을 만족해야 한다.
- 정사각형은 서로 겹치면 안 된다.
- 도형은 모두 연결되어 있어야 한다.
- 정사각형의 변끼리 연결되어 있어야 한다. 즉, 꼭짓점과 꼭짓점만 맞닿아 있으면 안 된다.
정사각형 4개를 이어 붙인 폴리오미노는 테트로미노라고 하며, 다음과 같은 5가지가 있다.

아름이는 크기가 N×M인 종이 위에 테트로미노 하나를 놓으려고 한다. 종이는 1×1 크기의 칸으로 나누어져 있으며, 각각의 칸에는 정수가 하나 쓰여 있다.
테트로미노 하나를 적절히 놓아서 테트로미노가 놓인 칸에 쓰여 있는 수들의 합을 최대로 하는 프로그램을 작성하시오.
테트로미노는 반드시 한 정사각형이 정확히 하나의 칸을 포함하도록 놓아야 하며, 회전이나 대칭을 시켜도 된다.
입력
첫째 줄에 종이의 세로 크기 N과 가로 크기 M이 주어진다. (4 ≤ N, M ≤ 500)
둘째 줄부터 N개의 줄에 종이에 쓰여 있는 수가 주어진다. i번째 줄의 j번째 수는 위에서부터 i번째 칸, 왼쪽에서부터 j번째 칸에 쓰여 있는 수이다. 입력으로 주어지는 수는 1,000을 넘지 않는 자연수이다.
출력
첫째 줄에 테트로미노가 놓인 칸에 쓰인 수들의 합의 최댓값을 출력한다.
이 문제의 알고리즘 분류는 구현, 브루트포스 알고리즘으로 되어있는데 나는 여기에 더해서 백트래킹으로 풀었다.
처음에는 BFS로 풀어야 하나 했지만 잘못 접근했다는 것을 깨닫고 급하게 백트래킹으로 노선을 바꾸게 되었다.

4칸씩 묶어야 하는데 그림에서 실수로 5칸씩 묶은 것도 몇 개 있다...
이것이 브루트포스라고 분류되는 이유는 2차원 배열의 모든 칸마다 4칸씩 묶을 수 있는 경우의 수를 모두 생각해야 하기 때문이다.
나는 이동 경로를 저장할 배열을 하나 생성하여 BFS로 풀려고 했으나 대단히 잘못된 생각이었다.

인접 칸 4개를 모으게 되면 여기서 합을 구한다.

맨 마지막에 합류하게 된 칸을 방문 체크 해제한 다음 다른 인접 칸으로 간다.
새로운 인접 칸 4개를 모으게 되었으니 여기서 합을 구한다.
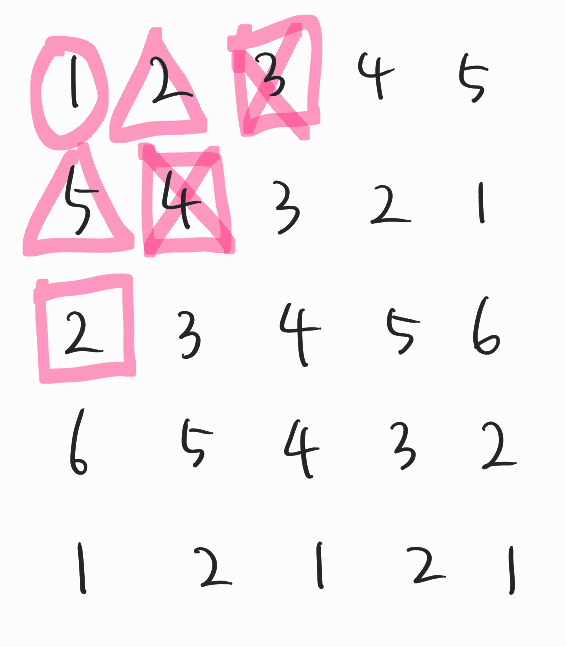
맨 마지막에 합류하게 된 칸을 방문 체크 해제한 다음 다른 인접 칸으로 간다.
새로운 인접 칸 4개를 모으게 되었으니 여기서 합을 구한다.
이 과정의 반복이다.
백트래킹으로 푼 이유는 이렇게 인접 칸 4개를 모으면 합을 더하고, 맨 마지막 칸을 방문 체크 해제한 다음 다른 인접 칸으로 가서 합을 더하고, 또 마지막 칸을 방문 체크 해제한 다음 다른 인접 칸으로 가서 합을 더하고....의 반복이기 때문이다.
이것을 코드로 바꾸면 다음과 같다.
참고로 checkFuckyouShapes 함수는 백트래킹으로 구할 수 없는 예외 모양을 처리하는 함수이다.
이 함수의 구현 코드를 보기 전에 dfs 구현 코드부터 보자.
그런데 여기서 끝이 아니다.
이 문제가 요구하는 것은 "구현" 능력이다.
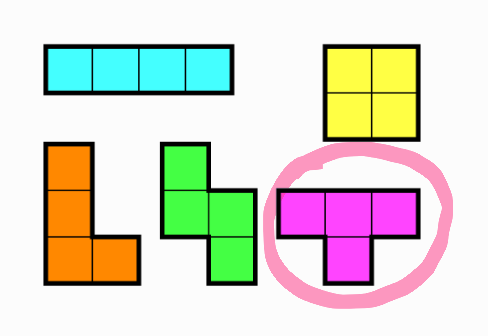
동그라미 친 모양의 합은 백트래킹으로는 절대 구할 수 없다.
예제 입력 3 복사
4 10
1 2 1 2 1 2 1 2 1 2
2 1 2 1 2 1 2 1 2 1
1 2 1 2 1 2 1 2 1 2
2 1 2 1 2 1 2 1 2 1
예제 출력 3 복사
7
이 예제가 바로 저 뻑큐 모양(ㅗ, ㅜ, ㅓ, ㅏ) 의 합을 구할 수 있냐고 힌트를 준 것이다.
그렇다면 어떻게 해야 하나?
ㅗ, ㅜ, ㅓ, ㅏ 모양들은 일일히 따로 합을 구해주어야 한다.
그래서 구현 문제인 것이다.
내가 자신없는 알고리즘이 구현인데 당분간 구현 문제 위주로 많이 풀어봐야 겠다.
위에서 나왔던 예외 모양 처리 함수가 바로 이것이다.
이 함수를 모든 칸 하나 하나를 탐색할 때마다 수행해주어야 한다.
그래서 이 문제가 구현이자 브루트포스 알고리즘인 것이다.
자, 그럼 이제 전체 코드를 보자.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
|
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class P14500_테트로미노 {
static int N, M; // 종이의 세로, 가로 크기
static int[] dx = {-1, 0, 1, 0}; // 상, 하 이동
static int[] dy = {0, -1, 0, 1}; // 좌, 우 이동
static int[][] paper; // 2차원 종이 배열
static boolean[][] visited; // 2차원 방문 체크 배열
static int maxSum; // 테트로미노가 놓인 칸에 쓰인 수들의 합의 최댓값
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
paper = new int[N][M];
visited = new boolean[N][M];
// 2차원 종이 배열 초기화
for (int i = 0; i < N; i++) {
st = new StringTokenizer(br.readLine());
for (int j = 0; j < M; j++) {
paper[i][j] = Integer.parseInt(st.nextToken());
}
}
// 모든 칸을 탐색
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++) {
visited[i][j] = true; // 현재 칸을 방문 체크
// 첫 번째 인자: 현재 칸의 x좌표
// 두 번째 인자: 현재 칸의 y좌표
// 세 번째 인자: 현재까지 계산된 칸에 쓰인 수들의 합 => 현재 칸에 적힌 수로 초기화
// 네 번째 인자: 현재까지 계산된 칸 개수 => 첫 번째 칸이므로 1
dfs(i, j, paper[i][j], 1);
visited[i][j] = false; // 현재 칸을 방문 해제 => 다음 칸으로 이동
// ㅗ, ㅜ, ㅓ, ㅏ 모양은 백트래킹으로 탐색이 불가능하므로 따로 처리
checkFuckyouShapes(i, j);
}
}
System.out.println(maxSum); // 테트로미노가 놓인 칸에 쓰인 수들의 합의 최댓값 출력
}
// sum: 현재까지 계산된 칸에 쓰인 수들의 합
// depth: 현재까지 계산된 칸 개수
public static void dfs(int x, int y, int sum, int depth) {
// 깊이(칸 개수)가 4가 되면 그동안 구했던 합과 최댓값 변수 중에서
// 더 큰 값을 최댓값 갱신 후 함수 종료
if (depth == 4) {
maxSum = Math.max(maxSum, sum);
return;
}
// 현재 칸의 상, 하, 좌, 우 탐색
for (int i = 0; i < 4; i++) {
int nx = x + dx[i]; // 인접 칸의 x좌표
int ny = y + dy[i]; // 인접 칸의 y좌표
// 인접 칸의 좌표가 유효 인덱스 범위에서 벗어난다면 건너뛰기
if (nx < 0 || ny < 0 || nx >= N || ny >= M) {
continue;
}
// 인접 칸을 방문하지 않았다면
if (!visited[nx][ny]) {
visited[nx][ny] = true; // 인접 칸을 방문 체크
// 첫 번째 인자: 인접 칸의 x좌표
// 두 번째 인자: 인접 칸의 y좌표
// 세 번째 인자: 현재까지 계산된 칸에 쓰인 수들의 합 => 인접 칸에 적힌 수를 더하기
// 네 번째 인자: 현재까지 계산된 칸 개수 => 1 증가
dfs(nx, ny, sum + paper[nx][ny], depth + 1);
visited[nx][ny] = false; // 인접 칸을 방문 해제 => 다음 칸으로 이동
}
}
}
// ㅗ, ㅜ, ㅓ, ㅏ 모양에 속하는 칸들의 수를 더하여 최댓값 변수 갱신
public static void checkFuckyouShapes(int x, int y) {
// ㅗ 모양
if (x >= 1 && y >= 1 && x < N && y < M - 1) {
int sum = paper[x][y] + paper[x - 1][y] + paper[x][y - 1] + paper[x][y + 1];
maxSum = Math.max(maxSum, sum);
}
// ㅜ 모양
if (x >= 0 && y >= 1 && x < N - 1 && y < M - 1) {
int sum = paper[x][y] + paper[x + 1][y] + paper[x][y - 1] + paper[x][y + 1];
maxSum = Math.max(maxSum, sum);
}
// ㅓ 모양
if (x >= 1 && y >= 1 && x < N - 1 && y < M) {
int sum = paper[x][y] + paper[x][y - 1] + paper[x - 1][y] + paper[x + 1][y];
maxSum = Math.max(maxSum, sum);
}
// ㅏ 모양
if (x >= 1 && y >= 0 && x < N - 1 && y < M - 1) {
int sum = paper[x][y] + paper[x][y + 1] + paper[x - 1][y] + paper[x + 1][y];
maxSum = Math.max(maxSum, sum);
}
}
static class Point {
int x, y;
Point(int x, int y) {
this.x = x;
this.y = y;
}
}
}
|
cs |
'알고리즘 > 백준' 카테고리의 다른 글
| [백준 / Java] 10026: 적록색약 (BFS) (0) | 2024.07.11 |
|---|---|
| [백준 / Java] 16236: 아기상어 (시뮬레이션, BFS) (0) | 2024.07.10 |
| [백준 / Java] 2146: 다리 만들기 (BFS) (1) | 2024.07.05 |
| [백준 / Java] 21736: 헌내기는 친구가 필요해 (BFS) (0) | 2024.07.05 |
| [백준 / Java] 20920: 영단어 암기는 괴로워 (자료구조) (0) | 2024.07.01 |




