자바칩
[백준 / Java] 2146: 다리 만들기 (BFS) 본문
난이도: Gold 3
문제: https://www.acmicpc.net/problem/2146
문제
여러 섬으로 이루어진 나라가 있다. 이 나라의 대통령은 섬을 잇는 다리를 만들겠다는 공약으로 인기몰이를 해 당선될 수 있었다. 하지만 막상 대통령에 취임하자, 다리를 놓는다는 것이 아깝다는 생각을 하게 되었다. 그래서 그는, 생색내는 식으로 한 섬과 다른 섬을 잇는 다리 하나만을 만들기로 하였고, 그 또한 다리를 가장 짧게 하여 돈을 아끼려 하였다.
이 나라는 N×N크기의 이차원 평면상에 존재한다. 이 나라는 여러 섬으로 이루어져 있으며, 섬이란 동서남북으로 육지가 붙어있는 덩어리를 말한다. 다음은 세 개의 섬으로 이루어진 나라의 지도이다.

위의 그림에서 색이 있는 부분이 육지이고, 색이 없는 부분이 바다이다. 이 바다에 가장 짧은 다리를 놓아 두 대륙을 연결하고자 한다. 가장 짧은 다리란, 다리가 격자에서 차지하는 칸의 수가 가장 작은 다리를 말한다. 다음 그림에서 두 대륙을 연결하는 다리를 볼 수 있다.

물론 위의 방법 외에도 다리를 놓는 방법이 여러 가지 있으나, 위의 경우가 놓는 다리의 길이가 3으로 가장 짧다(물론 길이가 3인 다른 다리를 놓을 수 있는 방법도 몇 가지 있다).
지도가 주어질 때, 가장 짧은 다리 하나를 놓아 두 대륙을 연결하는 방법을 찾으시오.
입력
첫 줄에는 지도의 크기 N(100이하의 자연수)가 주어진다. 그 다음 N줄에는 N개의 숫자가 빈칸을 사이에 두고 주어지며, 0은 바다, 1은 육지를 나타낸다. 항상 두 개 이상의 섬이 있는 데이터만 입력으로 주어진다.
출력
첫째 줄에 가장 짧은 다리의 길이를 출력한다.
골드3 치고는 꽤 어렵지 않게 풀었던 것 같다. 예전에는 골드3이면 몇 시간동안 혼자 싸움을 하다가 결국 답을 찾아봤었는데 2차원 배열 BFS 문제만 주구장창 풀어서 그런지 유형을 확실히 익히게 되어서 1시간 내로 문제를 풀 수 있었다.
일단 2차원 BFS 니까 문제에 주어진 배열을 저장할 map 2차원 배열과
각 칸을 방문 체크할 visited 2차원 배열은 무조건 필요하다.
그 외에도 선언해야할 배열이 있다. 아래를 보자.

이 문제의 핵심은 같은 섬에 해당하는 칸은 모두 같은 번호를 부여하는 것이다.
빨간색 구역에 해당하는 칸들은 모두 1으로 저장하고,
파란색 구역에 해당하는 칸들은 모두 2으로 저장하고,
초록색 구역에 해당하는 칸들은 모두 3으로 저장할 배열이 필요하다.
이 배열을 island 2차원 배열로 선언하고 값들을 저장하자.
코드는 위와 같다.
BFS는 같은 육지에서만 탐색하다가 육지를 벗어나면 알아서 BFS 수행이 끝난다.
그러므로 해당 칸을 방문을 하지 않았거나 해당 칸이 육지인 칸을 발견했을 때 그 칸부터 BFS 수행하면 섬 한 개만 탐색하는 것이 된다.
새로운 섬을 발견할 때마다 섬 번호를 1 증가하고 그 섬에 해당하는 칸들에 모두 같은 섬 번호를 부여하면 된다.
divideIsland 함수는 섬을 나누는 함수이다.
함수로 따로 빼는 이유는 코드의 복잡성을 줄여주고 가독성을 높여주기 위함이다.
만약 아래 코드가 저 2중 for문 내에 있었다면 들여쓰기가 너무 많이 되어서 매우 복잡해보이는 코드가 되었을 것이다.
함수를 만들면 나중에 수정할 때 더 보기 편해진다.
2차원 배열 BFS 알고리즘을 잘 알고 있다면 익숙한 코드일 것이다.
섬 번호를 인자로 넘겨주어서 BFS 수행 중일 때 육지에 해당하는 칸에는 모두 같은 섬 번호를 부여해주면 된다.
이제 구역 나누기를 끝냈다.
다음으로 해야할 일은 가장자리를 찾는 것이다.
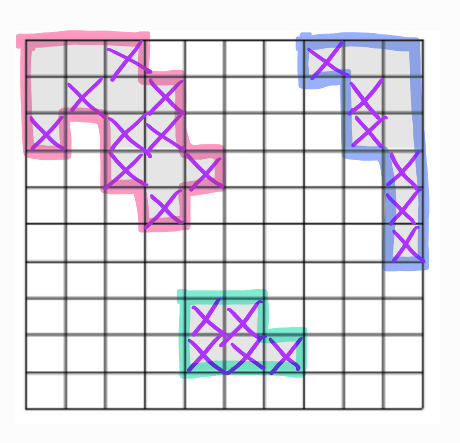
육지인 칸을 탐색해서 해당 칸의 상하좌우 중에서 한 면이라도 바다랑 맞닿아있다면 해당 칸은 가장자리인 것이다.
ArrayList 타입의 edges 를 선언하여 가장자리를 찾고 좌표 저장을 여기에 해주면 된다.
findEdge 함수는 해당 칸을 기준으로 상하좌우를 탐색하여 해당 칸이 가장자리인지 찾는 함수이다.
만약 해당 칸이 가장자리라면 edges 리스트에 칸 좌표를 추가한다.
참고로 여기에서 사용되는 dx, dy 배열은 다음과 같다.
int[] dx = {-1, 0, 1, 0} // 상, 하 이동
int[] dy = {0, -1, 0, 1} // 좌, 우 이동
같은 인덱스끼리는 세트이다.
즉, (-1, 0), (0, -1), (1, 0), (0, 1) 만큼 이동을 시켜주는 것이다.
이 배열은 2차원 배열 BFS에서 정말 많이 쓰이니까 외워두자.
이제 가장자리 칸들만 탐색해서 각 가장자리 당 다음 구역까지의 최단거리를 구하면 된다.
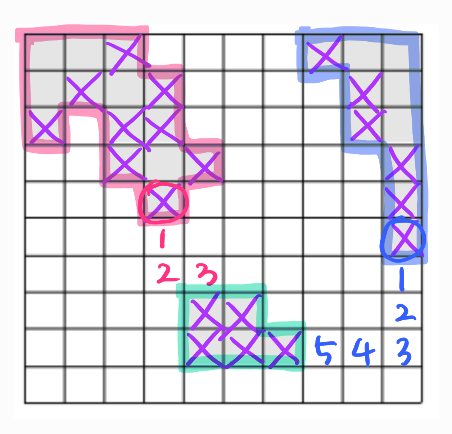
위에서 표시해둔 가장자리 칸들만 탐색해서 다음 구역까지의 거리를 구해서 최단거리 변수에 갱신하면 된다.
참고로 이 문제의 최단 거리는 3이다.
bfs 함수는 해당 가장자리 칸을 기준으로 다음 섬까지의 거리를 찾아서 최단거리 변수에 갱신하는 함수이다.
다음 섬까지의 거리를 구하는 방법은 이전 칸까지의 거리 + 1을 하면 된다.
BFS로 옮긴 칸이 육지이고, 시작 칸과 옮긴 칸의 island 배열에 저장된 섬 번호가 다르다면 다른 섬에 도착한 것이므로 시작 칸과 옮긴 칸 바로 전까지의 거리를 구해서 최단거리 변수에 갱신하면 된다.
이 코드도 BFS 알고리즘을 잘 알고 있다면 익숙한 코드이다.
2차원 배열 BFS 문제들은 몇줄 정도만 잘 변형시키면 다 풀리는 문제이다.
마지막으로 최종 갱신된 최단거리 변수(minLength)를 출력하면 된다.
사실 가장자리를 일일히 저장하지 않고 처음부터 모든 칸을 탐색해서 거리를 구하는 방법도 있지만,
그렇게 하면 시간이 매우 많이 소요된다.
모든 칸을 탐색하면 2중 for문을 돌려서 시간 복잡도가 O(N^2)이지만
가장자리 칸들만 담긴 리스트들을 탐색하면 1중 for문만 돌려서 시간 복잡도가 O(N)밖에 안되기 때문이다.
필자는 두 가지 방법 다 해보았는데 소요 시간이 상당히 많이 차이나는 것을 확인할 수 있었다.

자, 이제 최종 코드를 보자.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
|
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;
public class P2146_다리만들기 {
static int N; // 지도의 크기
static int[] dx = {-1, 0, 1, 0}; // 상, 하 이동
static int[] dy = {0, -1, 0, 1}; // 좌, 우 이동
static int[][] map; // 2차원 지도 배열
static boolean[][] visited; // 2차원 방문 체크 배열
static int[][] island; // 2차원 섬 배열
static ArrayList<Point> edges = new ArrayList<>(); // 가장자리 좌표 리스트
static int minLength = Integer.MAX_VALUE; // 가장 짦은 다리의 길이
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(br.readLine());
map = new int[N][N];
visited = new boolean[N][N];
island = new int[N][N];
// 2차원 지도 배열 초기화
for (int i = 0; i < N; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
for (int j = 0; j < N; j++) {
// 0: 바다, 1: 육지
map[i][j] = Integer.parseInt(st.nextToken());
}
}
int islandNum = 0; // 섬 번호 (섬이 다르면 다른 번호)
// 모든 칸을 탐색
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
// 해당 칸을 방문하지 않았거나, 해당 칸이 육지일 때
if (!visited[i][j] && map[i][j] == 1) {
islandNum++; // 섬 번호 1 증가
divideIsland(i, j, islandNum); // 섬 나누기
}
}
}
// 모든 칸을 탐색
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
if (map[i][j] == 1) { // 해당 칸이 육지일 때
// 해당 칸이 가장자리인지 찾고, 가장자리라면 해당 좌표를 리스트에 추가
findEdge(i, j);
}
}
}
// 가장자리 칸들만 탐색
for (Point edge : edges) {
// 가장자리마다 거리를 다르게 계산해야 하므로 방문 배열은 칸마다 초기화
visited = new boolean[N][N];
bfs(edge.x, edge.y); // 해당 가장자리 칸부터 bfs 수행
}
System.out.println(minLength); // 가장 짧은 다리의 길이를 출력
}
// 섬 나누기
public static void divideIsland(int a, int b, int islandNum) {
Queue<Point> queue = new LinkedList<>(); // bfs 수행을 위한 큐
queue.add(new Point(a, b)); // 큐에 시작 칸 삽입
visited[a][b] = true; // 시작 칸을 방문 체크
island[a][b] = islandNum; // 시작 칸에 섬 번호 부여
// 큐가 빌 때까지 반복
while (!queue.isEmpty()) {
Point now = queue.poll(); // 큐에서 현재 칸을 뽑기
// 현재 칸 기준으로 상, 하, 좌, 우 탐색
for (int i = 0; i < 4; i++) {
int x = now.x + dx[i]; // 인접 칸의 x좌표
int y = now.y + dy[i]; // 인접 칸의 y좌표
// 인접 칸의 인덱스가 유효 범위에 속하지 않는다면 건너뛰기
if (x < 0 || y < 0 || x >= N || y >= N) {
continue;
}
// 인접 칸을 이미 방문했거나 인접 칸이 바다라면 건너뛰기
if (visited[x][y] || map[x][y] == 0) {
continue;
}
queue.add(new Point(x, y)); // 큐에 인접 칸 삽입
visited[x][y] = true; // 인접 칸을 방문 체크
island[x][y] = islandNum; // 인접 칸에 섬 번호 부여
}
}
}
// 현재 칸의 상하좌우를 탐색하여 가장자리인지 찾기
public static void findEdge(int a, int b) {
for (int i = 0; i < 4; i++) {
int x = a + dx[i]; // 인접 칸의 x좌표
int y = b + dy[i]; // 인접 칸의 y좌표
// 인접 칸의 인덱스가 유효 범위에 속하지 않는다면 건너뛰기
if (x < 0 || y < 0 || x >= N || y >= N) {
continue;
}
if (map[x][y] == 0) { // 인접 칸이 바다라면 해당 칸은 가장자리
edges.add(new Point(a, b)); // 가장자리 리스트에 인접 칸의 좌표 추가 후
break; // 가장자리를 이미 찾았으므로 반복문 탈출 => 함수 종료
}
}
}
// 가장자리 칸부터 다음 구역까지의 거리를 구하고 가장 짧은 다리의 길이 찾기
public static void bfs(int a, int b) {
Queue<Point> queue = new LinkedList<>(); // bfs 수행을 위한 큐
int[][] distance = new int[N][N]; // 2차원 거리 저장 배열
queue.add(new Point(a, b)); // 큐에 가장자리 칸 삽입
visited[a][b] = true; // 가장자리 칸을 방문 체크
// 큐가 빌 때까지 반복
while (!queue.isEmpty()) {
Point now = queue.poll(); // 큐에서 현재 칸을 뽑기
// 현재 칸 기준으로 상, 하, 좌, 우 탐색
for (int i = 0; i < 4; i++) {
int x = now.x + dx[i]; // 인접 칸의 x좌표
int y = now.y + dy[i]; // 인접 칸의 y좌표
// 인접 칸의 인덱스가 유효 범위에 속하지 않거나,
// 인덱스가 유효 범위에 속하지만 이미 방문한 칸이라면 건너뛰기
if ((x < 0 || y < 0 || x >= N || y >= N) || visited[x][y]) {
continue;
}
// 인접 칸이 육지이고, 인접 칸의 섬 번호와 시작 칸의 섬 번호가 다르다면
// 두 칸은 다른 섬이므로 다리 연결 가능
if (map[x][y] == 1 && island[x][y] != island[a][b]) {
// 현재 가장 짧은 다리의 길이와 현재 칸(인접 칸의 바로 이전 칸)까지의 거리 중에서
// 더 짧은 길이를 가장 짧은 다리의 길이에 갱신 후
minLength = Math.min(minLength, distance[now.x][now.y]);
return; // bfs 종료
}
queue.add(new Point(x, y)); // 큐에 인접 칸 삽입
visited[x][y] = true; // 인접 칸을 방문 체크
// 인접 칸까지의 거리 = 현재 칸까지의 거리 + 1
distance[x][y] = distance[now.x][now.y] + 1;
}
}
}
static class Point {
int x, y;
Point(int x, int y) {
this.x = x;
this.y = y;
}
}
}
|
cs |
'알고리즘 > 백준' 카테고리의 다른 글
| [백준 / Java] 16236: 아기상어 (시뮬레이션, BFS) (0) | 2024.07.10 |
|---|---|
| [백준 / Java] 14500: 테트로미노 (구현, 백트래킹) (0) | 2024.07.06 |
| [백준 / Java] 21736: 헌내기는 친구가 필요해 (BFS) (0) | 2024.07.05 |
| [백준 / Java] 20920: 영단어 암기는 괴로워 (자료구조) (0) | 2024.07.01 |
| [백준 / Java] 16953: A → B (BFS) (0) | 2024.06.29 |



